In this section, we will briefly talk about the arithmetic functions in the PyTorch. Then, we will introduce the axis parameter in most of these functions in detail.
Finally, we talk about indexing the tensor, which is very tricky in manipulating the tensors as well.
Tensor functions
PyTorch supports many arithmetic functions for tensor. They are vectorized and acts very similar to numpy. (So if you are not familiar with numpy, learn it first). In the following, I’ll introduce some functions with the official docs.
binary arithmetic functions, such as
+, -, *, /, @etc. Entry-wise operations, supports broadcasting.binary logical functions, such as
torch.bitwise_and(),torch.bitwise_or…math functions, such as
exp, log, sigmoidetc.comparison functions, such as
torch.eq,torch.ge. The==and>=operators are overloaded, so they have the same effect.reduction functions. They are usually very useful. e.g.,
mean,median,argmax,sum… They do the corresponding operations on a specific dimension, requiring the “dim” parameter (See below).…… For more functions, please visit the docs.
Key: What is the “dim” parameter?
For the reduction functions such as argmax, we need to pass a parameter called dim. What does it mean?
The default value or
dimisNone, indicates that do theargmaxfor all the entries.On the other hand, if we specifies the
dimparameter, that means, we apply the functionargmaxon each vector along a specific “axis”. For all of the example below, we use a4x3x43D tensor.
1 | # create a 4x3x4 tensor |
- Then, in the first case, we do:
1 | a1 = torch.argmax(a, dim=0) |
See the gif below. If we set dim=0, that means, we apply the argmax function on each yellow vector (they are in the direction of dim0). The original tensor’s shape is 4x3x4, we reduce on the dim0, so now it’s 3x4, containing all results from argmax on the yellow vectors.
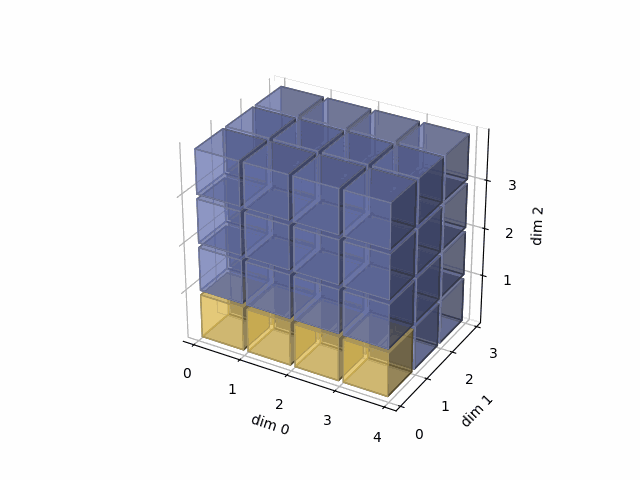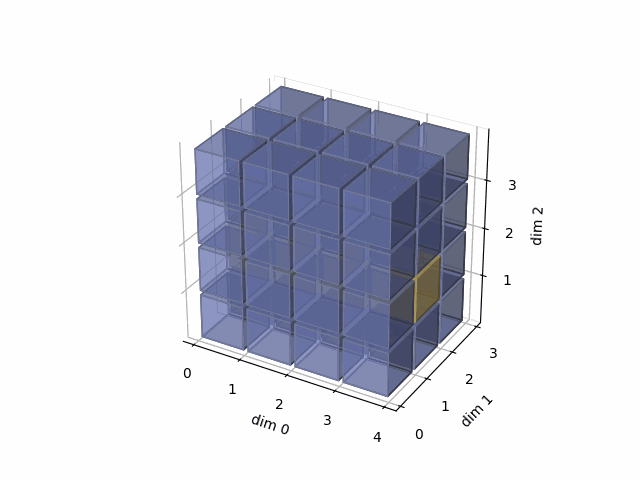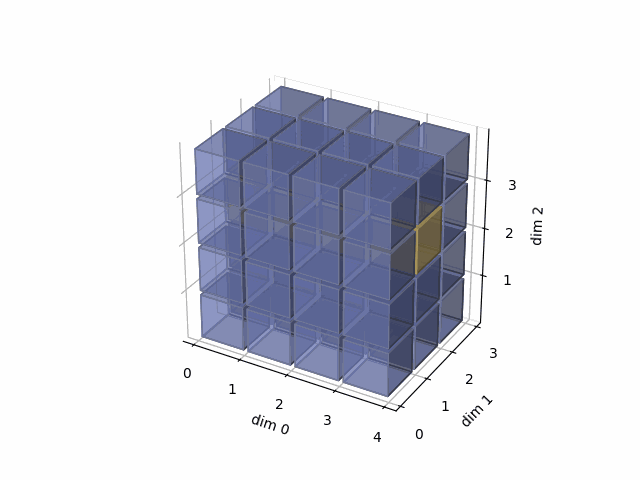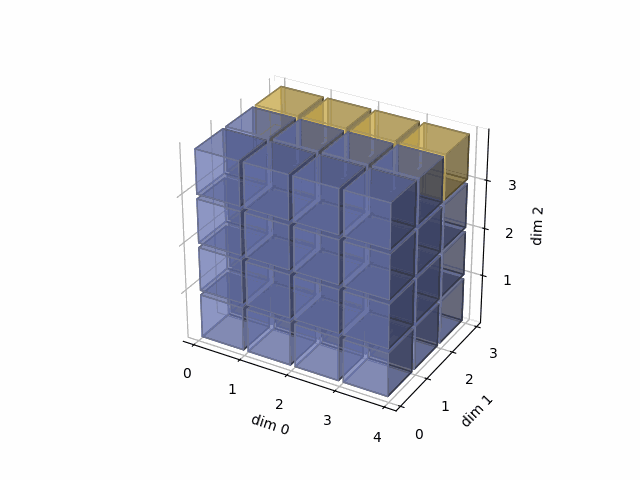
- Then, in the second case, we do:
1 | a2 = torch.argmax(a, dim=1) |
See the gif below. If we set dim=1, that means, we apply the argmax function on each yellow vector (they are in the direction of dim1). The original tensor’s shape is 4x3x4, we reduce on the dim1, so now we will have a result with 4x4 shape.
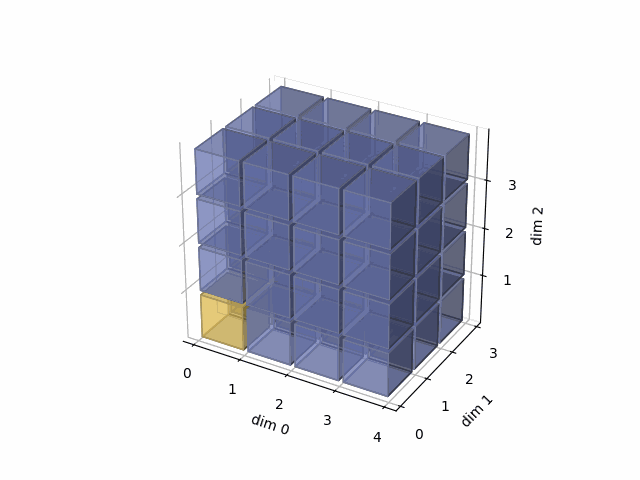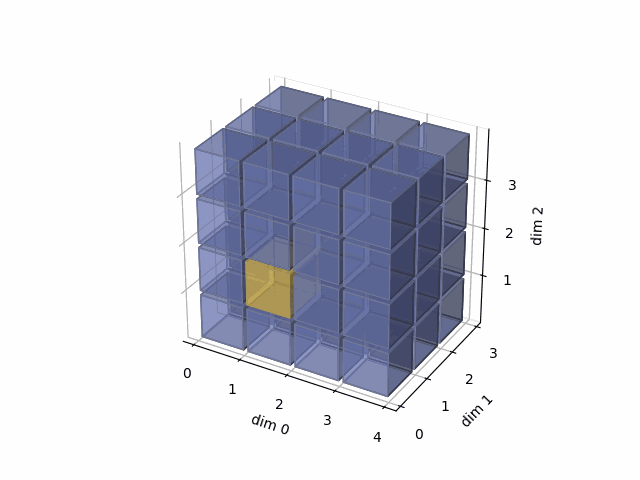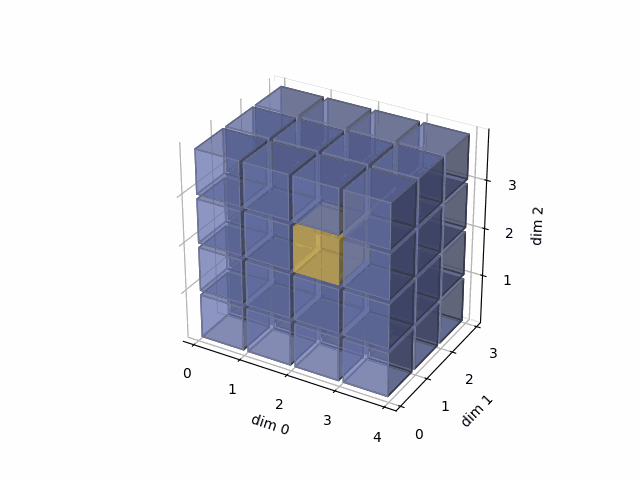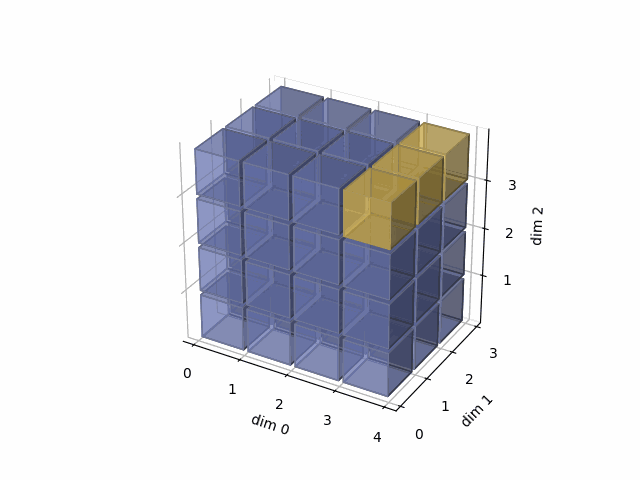
- Then, in the third case, we do:
1 | a3 = torch.argmax(a, dim=2) |
See the gif below. If we set dim=2, that means, we apply the argmax function on each yellow vector (they are in the direction of dim2). The original tensor’s shape is 4x3x4, we reduce on the dim2, so now we will have a result with 4x3 shape.
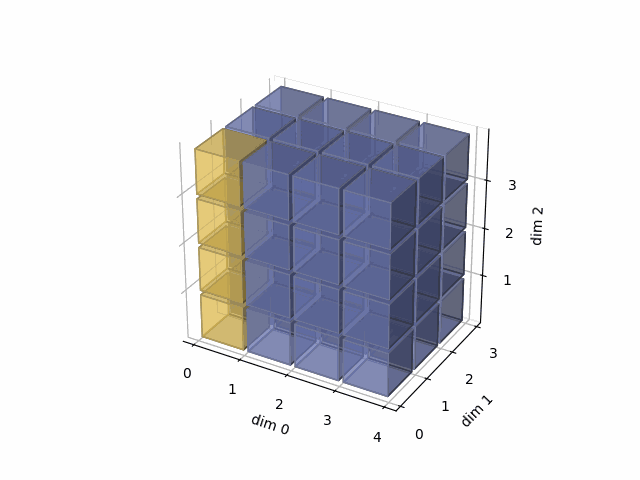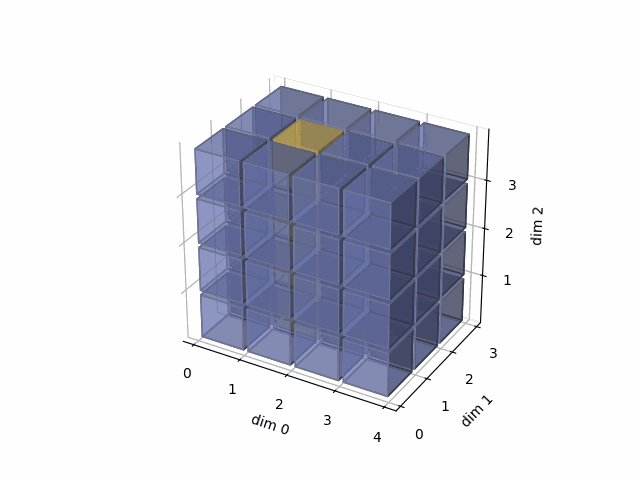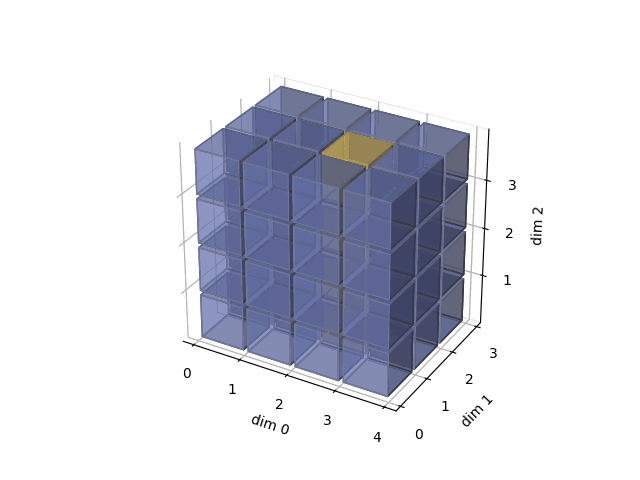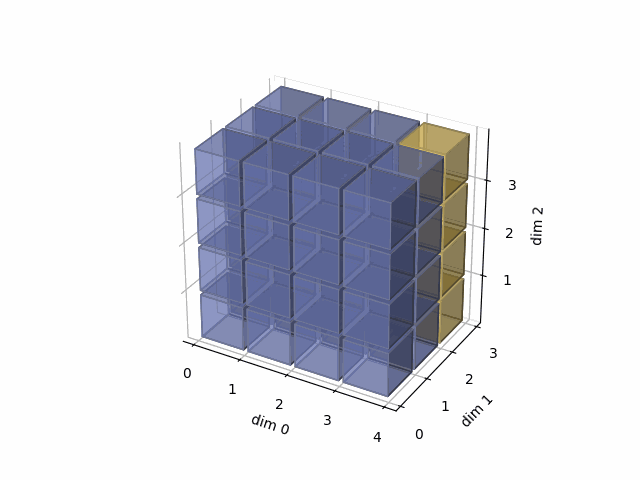
As member function
Many functions mentioned above has member function style. For example, the following pairs are equivalent.
1 | a = torch.randn(3, 4) |
As in-place function
The functions mentioned above returns a new result tensor, keeping the original one same. In some cases, we can do in-place operation on the tensor. The in-place functions are terminated with a _.
For example, the following pairs are equivalent.
1 | a = torch.randn(3, 4) |
Tensor indexing
Indexing is very powerful in torch. They are very similar to the one in numpy. Learn numpy first if you are not familiar with it.
1 | a = torch.randn(4, 3) |
The indexing supports many types, you can pass:
An integer.
a[1, 2]returns just one value 0-D tensortensor(0.9603), one element at (row 1, col 2).A Slice.
a[1::2, 2]returns 1-D tensortensor([0.9603, 1.4112]), two elements at (row 1, col 2) and (row 3, col 2).A colon. colon means everything on this dim.
a[:, 2]returns 1-D tensortensor([-3.5945, 0.9603, 1.5980, 1.4112]), a column of 4 elements at col 2.A None. None is used to create a new dim on the given axis. E.g.,
a[:, None, :]has the shape oftorch.Size([4, 1, 3]). A further example:
a[:, 2] returns 1-D vector tensor([-3.5945, 0.9603, 1.5980, 1.4112]) of col 2.
a[:, 2, None] returns 2-D vector tensor([[-3.5945], [0.9603], [1.5980], [1.4112]]) of col 2, which the original shape is kept.
A
...(Ellipsis). Ellipsis can be used as multiple:. E.g.,1
2
3
4a = torch.arange(16).reshape(2,2,2,2)
# The following returns the same value
a[..., 1]
a[:, :, :, 1]