PyTorch Practical Hand-Written Modules Basics 7--Mathematics Derivation of Linear Layer

In the section 6 to 9, we’ll investigate how to use torch.autograd.Function to implement the hand-written operators. The tentative outline is:

• In the last section (6), we talk about the basics of torch.autograd.Function. The operators defined by torch.autograd.Function can be automatically back-propagated.
• In this section (7), we’ll talk about mathematic derivation for the “linear layer” operator.
• In the section 8, we talk about writing C++ CUDA extension for the “linear layer” operator.
• In the section 9, we talk details about building the extension to a module, as well as testing. Then we’ll conclude the things we’ve done so far.

The linear layer is defined by Y = XW + b. There is a matrix multiplication operation, and a bias addition. We’ll talk about their forward/backward derivation separately.

(I feel sorry that currently there is some problem with displaying mathematics formula here. I’ll use screenshot first.)

Matrix multiplication: forward

The matrix multiplication operation is a common operator. Each entry in the result matrix is a vector dot product of two input matrixes. The (i, j) entry of the result is from multiplying first matrix’s row i vector and the second matrix’s column j vector. From this property, we know that number of columns in the first matrix should equal to number of rows in the second matrix. The shape should be: [m, n] x [n, r] -> [m, r]. For more details, see the figure illustration below.

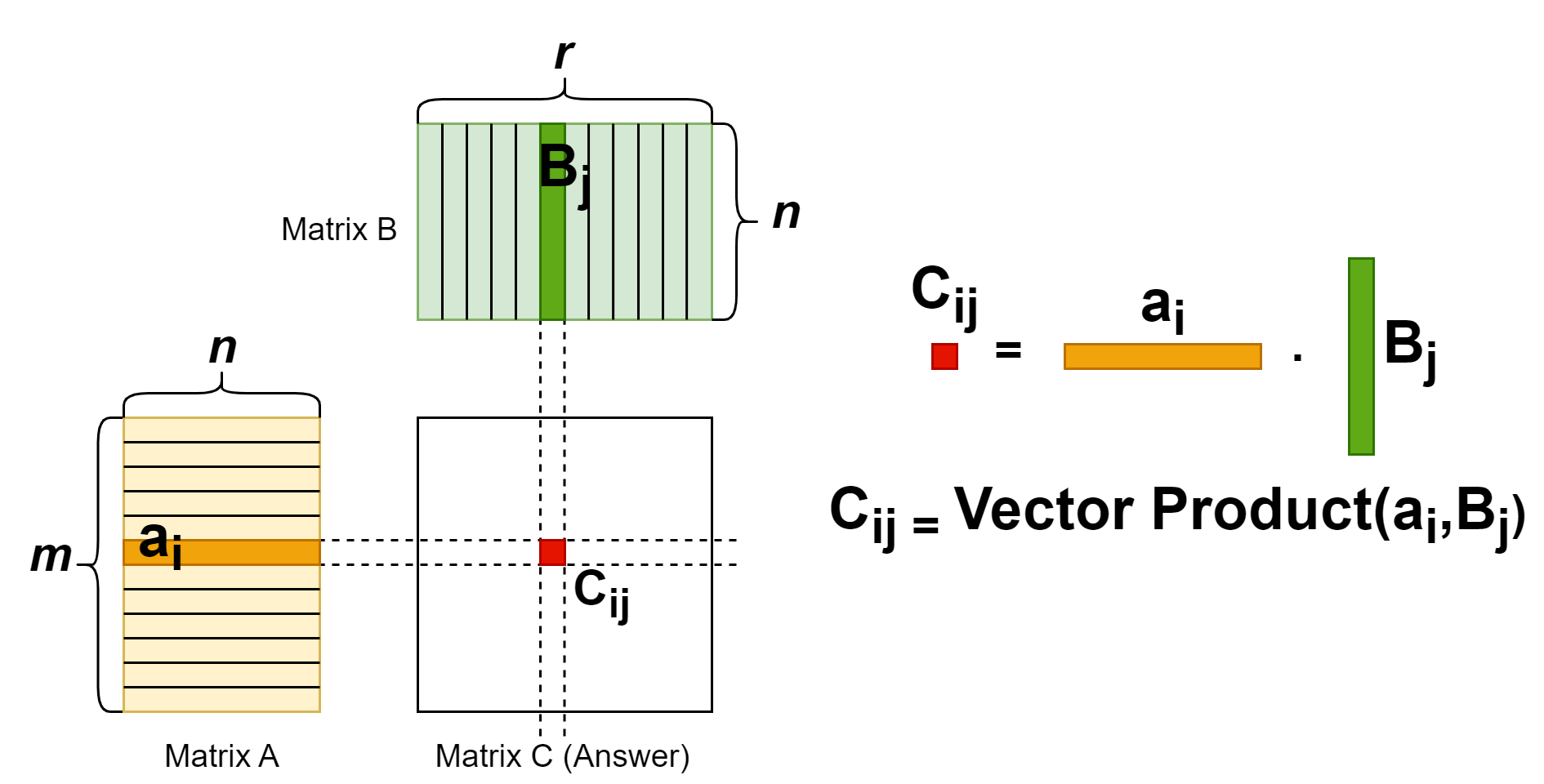
Matrix multiplication: backward

First, we should know what’s the goal of the backward propagation. In the upstream side, we would get the gradient of the answer matrix, C. (The gradient matrix has the same size as its corresponding matrix. i.e., if C is in shape [m, r], then gradient of C is shape [m, r] as well.) In this step, we should get the gradient of matrix A and B. Gradient of matrix A and B are functions in terms of matrix A and B and gradient of C. Specially, by chain rule, we can formulate it as

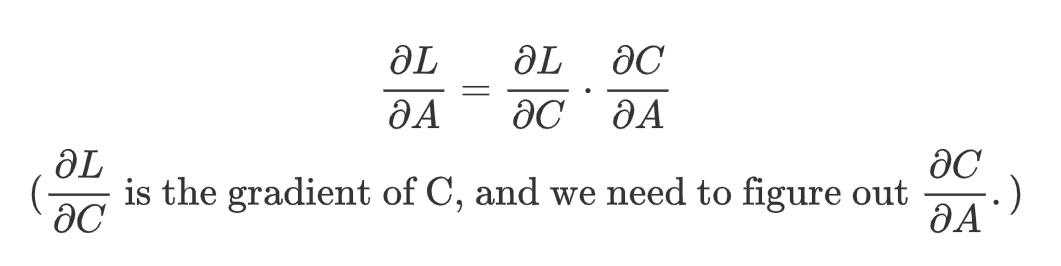
To figure out the gradient of A, we should first investigate how an entry A[i, j] contribute to the entries in the result matrix C. See the figure below:

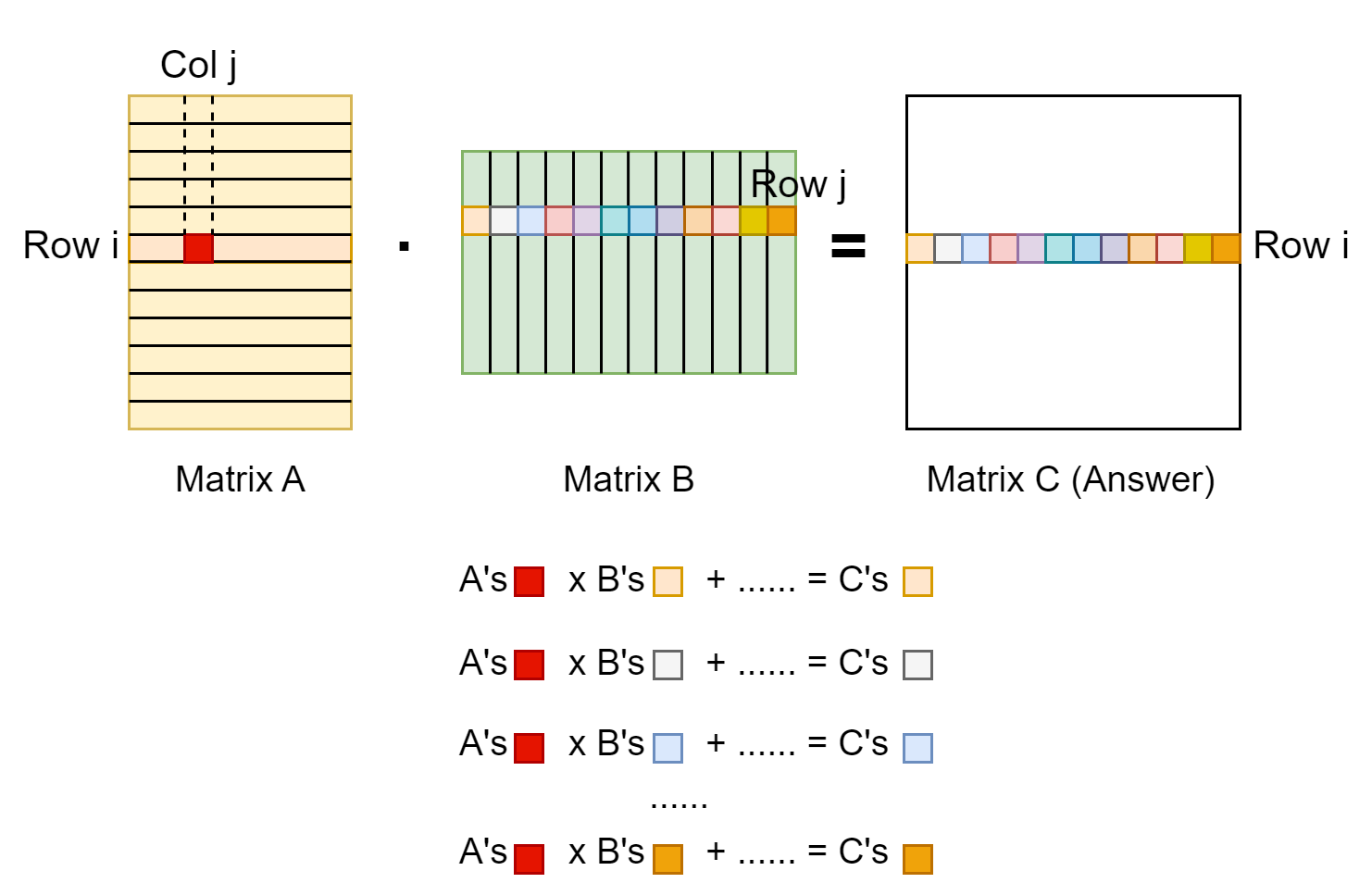
As shown above, entry A[i, j] multiplies with entries in row j of matrix B, contributing to the entries in row i of matrix C. We can write the gradient down in mathematics formula below:

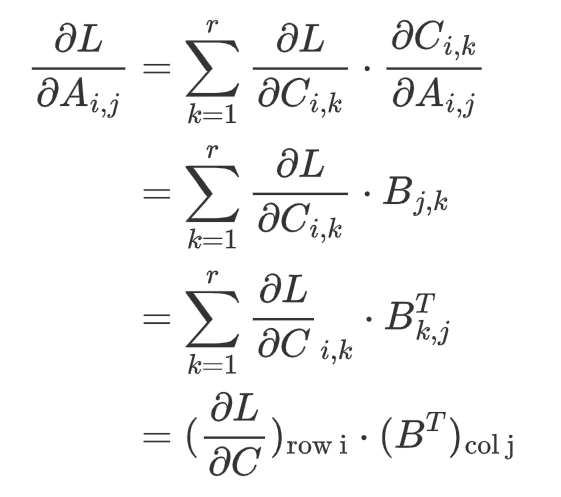
The result above is the gradient for one entry A[i, j], and it’s a vector dot product between a matrix’s row i and another matrix’s column j. Observing this formula, we can naturally extend it to the gradient of the whole matrix A, and that will be a matrix product.

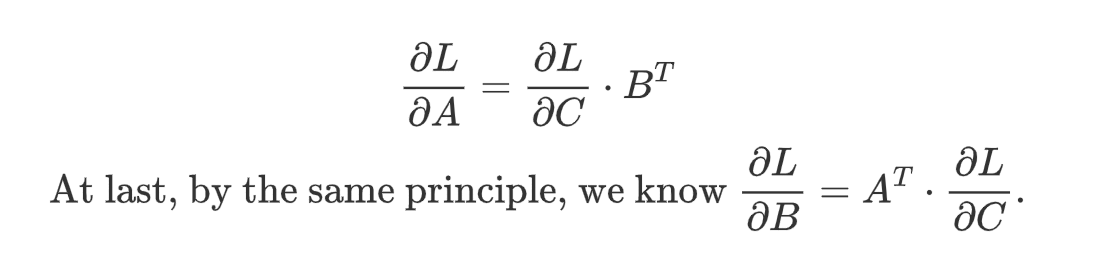
Recall “Gradient of matrix A and B are functions in terms of matrix A and B and gradient of C” we said before. Our derivation indeed show that, uh?

Add bias: forward

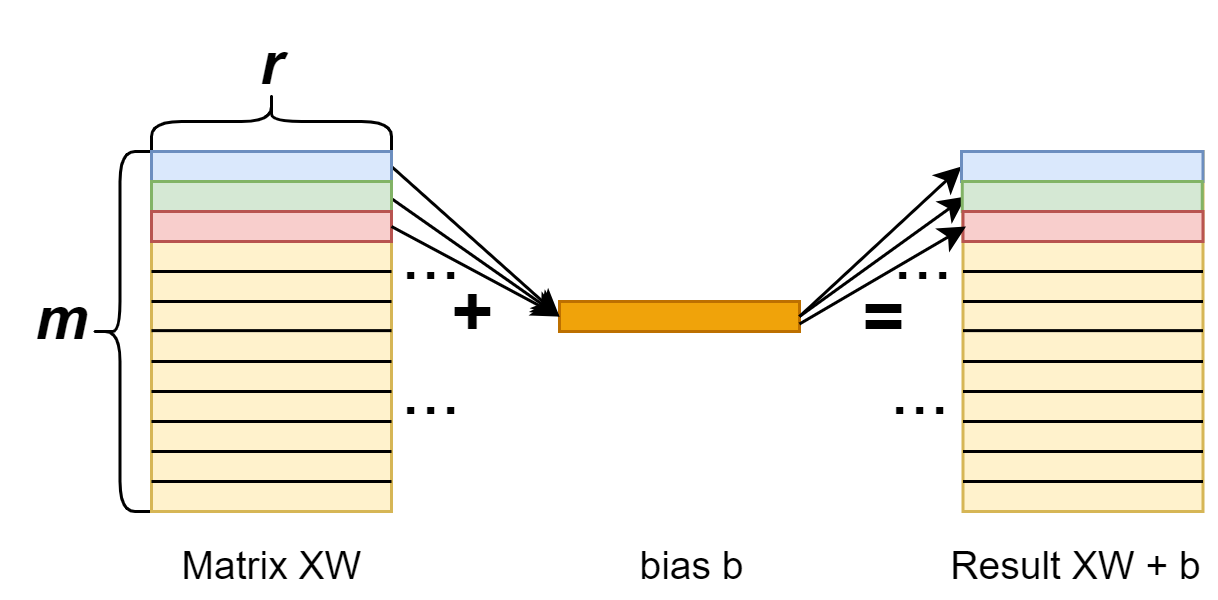
First, we should note that when doing the addition, we’re actually adding the XW matrix (shape [n, r]) with the bias vector (shape [r]). Indeed we have a broadcasting here. We add bias to each row of the XW matrix.

Add bias: backward

With the similar principle, we can get the gradient for the bias as well.

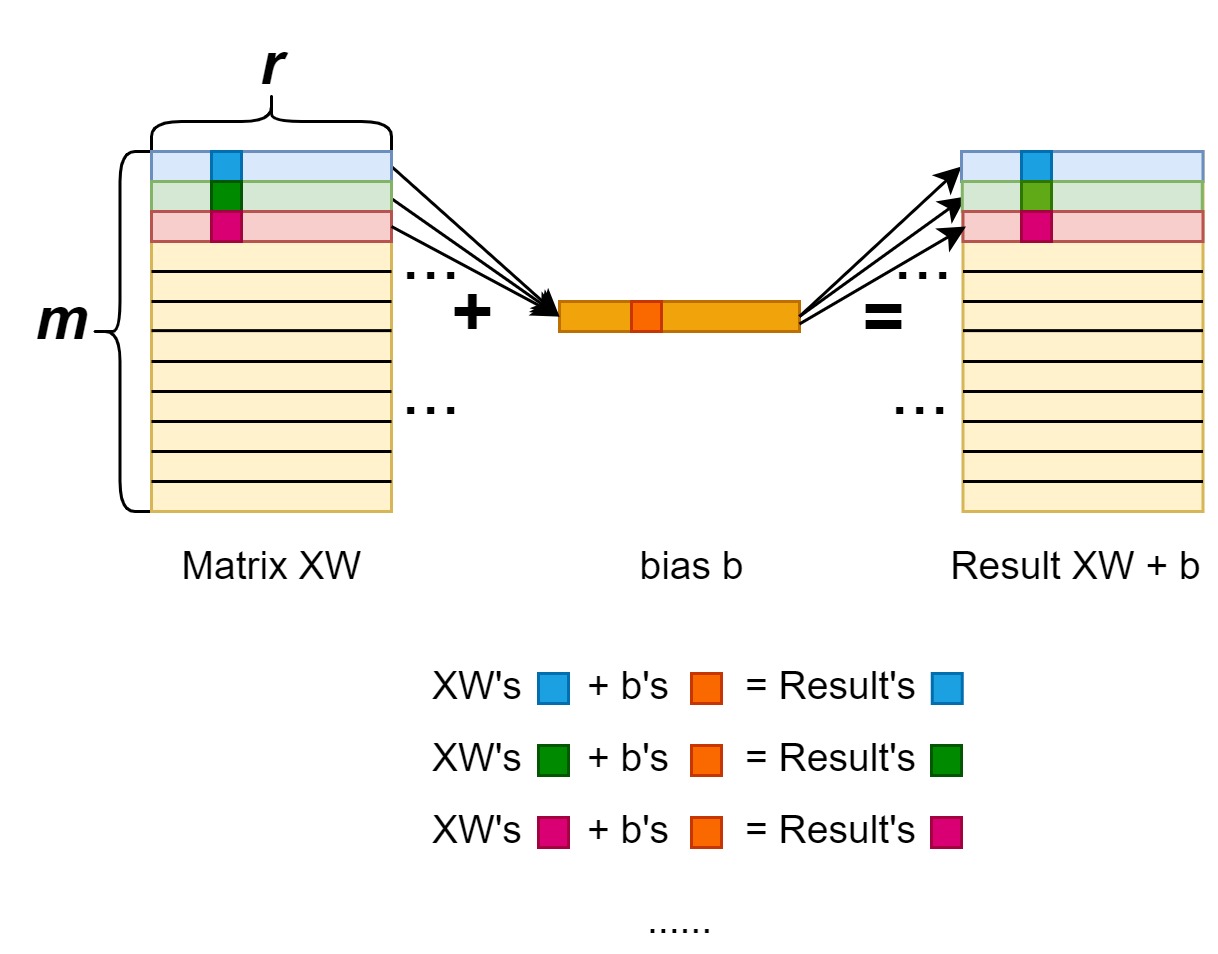
For each entry in vector b, the gradient is:

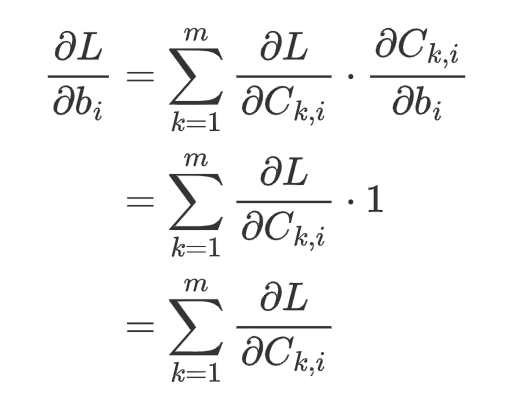
That is, the gradient of entry b_i is the summation of the i-th column. In total, the gradient will be the summation along each column (i.e., axis=0). In programming, we write:

grad_b = torch.sum(grad_C, axis=0)

PyTorch Verification

Finally, we can write a PyTorch program to verify if our derivation is correct: we will compare our calculated gradients with the gradients calculated by the PyTorch. If they are same, our derivation would be correct.

import torch
A = torch.randn(10, 20).requires_grad_()
B = torch.randn(20, 30).requires_grad_()

res = torch.mm(A, B)
res.retain_grad()
res.sum().backward()

print(torch.allclose(A.grad, torch.mm(res.grad, B.t()))) # grad_A = grad_res * B^T
print(torch.allclose(B.grad, torch.mm(A.t(), res.grad))) # grad_B = A^T * grad_res

Finally, the output is:

True
True

Which means that our derivation is correct.